Diffusion Impedance

1131 words (6 min) Matthew Lacey 28 Mar 2023

Overview

Mass transport processes, such as diffusion, migration and convection, are a key aspect of electrochemical systems. In this subsection, we will look at fundamental models for the effect of diffusion processes on impedance. As with the CPE, we invent some new circuit elements to describe these, but these can be approximated using the familiar resistors and capacitors, as we will see.

Semi-infinite diffusion

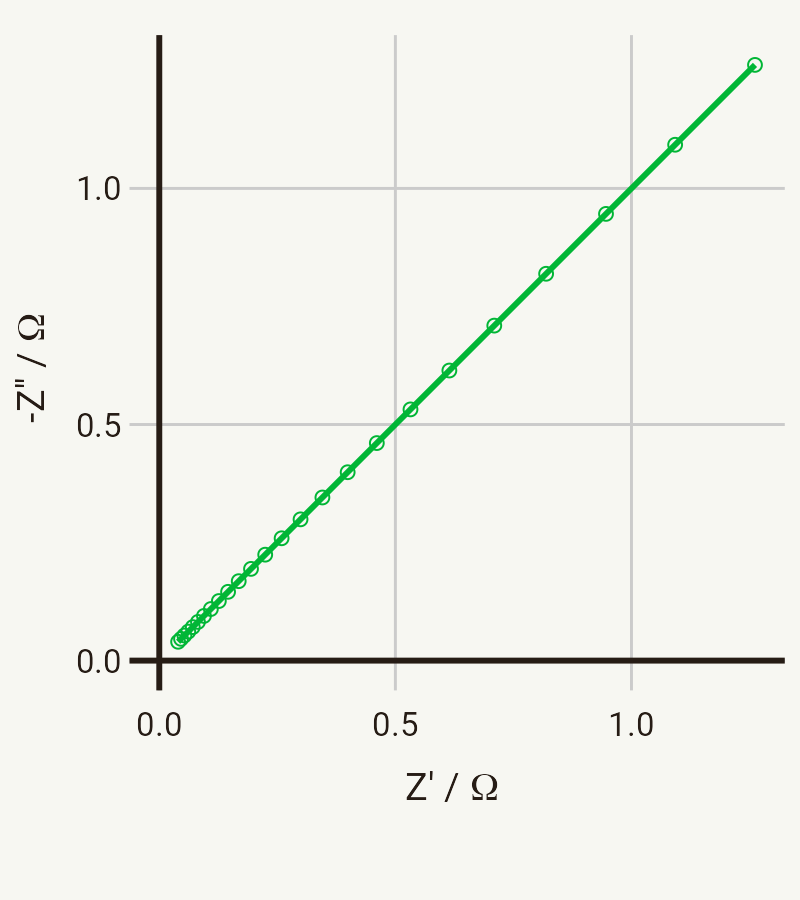
The simplest and most common circuit element for modelling diffusion behaviour is the Warburg impedance or Warburg element, which models semi-infinite linear diffusion – that is, diffusion in one dimension which is only bounded by a large planar electrode on one side.

The equation for this element is relatively simple:

Z Z_{W} = σ ω^{- 1 / 2} - j σ ω^{- 1 / 2}

where $σ$ is the Warburg coefficient, with units of Ω s^-1/2 – we’ll come back to this shortly. In the Nyquist plot, the Warburg impedance gives a straight line with a phase of 45°, which is very recognisable in EIS. If you spot a 45° line in the Nyquist plot, it is usually associated with diffusion. The below plot shows the Nyquist plot for a Warburg element with $σ$ of 10 Ω s^-1/2 in the frequency range 10 kHz - 10 Hz.

And if you’re looking at this thinking that this line look very much like a constant phase element but with a phase angle of 45°, then you’d be right – mathematically they are very much the same. In fact, some popular impedance analysis softwares do not actually provide a semi-infinite Warburg element, so a convenient alternative for this is a CPE element with n fixed at 0.5. This gives slightly different numbers back when fitting – if you use a CPE, you will get back the Q₀ value, rather than the Warburg coefficient $σ$ . The two values are related though, by the equation:

σ = \frac{1}{\sqrt{2} \cdot Q_{0}}

But what does $σ$ actually mean? This is somewhat more complicated, but if you consider the case where you have a soluble redox couple in solution, with a nice reversible electrochemical reaction like:

{O + n e}^{-} ⇌ R

then $σ$ is related to the diffusion coefficients and concentrations of those species:

σ = \frac{R T}{n^{2} F^{2} A \sqrt{2}} (\frac{1}{D_{O}^{1 / 2} c_{O}^{\infty}} + \frac{1}{D_{R}^{1 / 2} c_{R}^{\infty}})

here, in addition to the usual constants, $D_{O}$ and $D_{R}$ are the diffusion coefficients and $c_{O}^{\infty}$ and $c_{R}^{\infty}$ are the bulk concentrations for the species O and R respectively.

The transmission line

Conventional “Fickian” diffusion is not the only process which gives rise to this type of impedance in electrochemical systems. In batteries, the porosity of electrodes also gives rise to a similarly characteristic 45° line in the Nyquist plot.

This was described in detail by de Levie, who proposed the transmission line model for an electrode with cylindrical pores filled with electrolyte:

Consider the two parallel “rails” as being the electronic resistance in the electrode material itself and the ionic resistance in the electrolyte respectively. The capacitors represent the double layer capacitance.

This equivalent circuit, when infinitely long, gives an impedance response which is identical to the Warburg impedance above. Practically, however, porous electrodes have a finite length, and so show a 45° line only in a certain frequency range. The impedance response due to finite diffusion is discussed below.

A final point on the transmission line: if the transmission line shows the same response as Fickian diffusion, can the case of a porous electrode be considered diffusion as well? In a sense, yes. The movement of ions through the pores is coupled to the movement of electrons through the pore walls. This is an example of ambipolar diffusion.

Finite diffusion

Often in the “classic” electrochemical setups, diffusion often appears semi-infinite because the timescale of the experiment is not long enough for the system to reach a steady state. However, in many real systems and in some standard experiments, diffusion is either naturally, or by design, limited. This gives rise to finite diffusion behaviour, which shows a different response than the standard Warburg impedance.

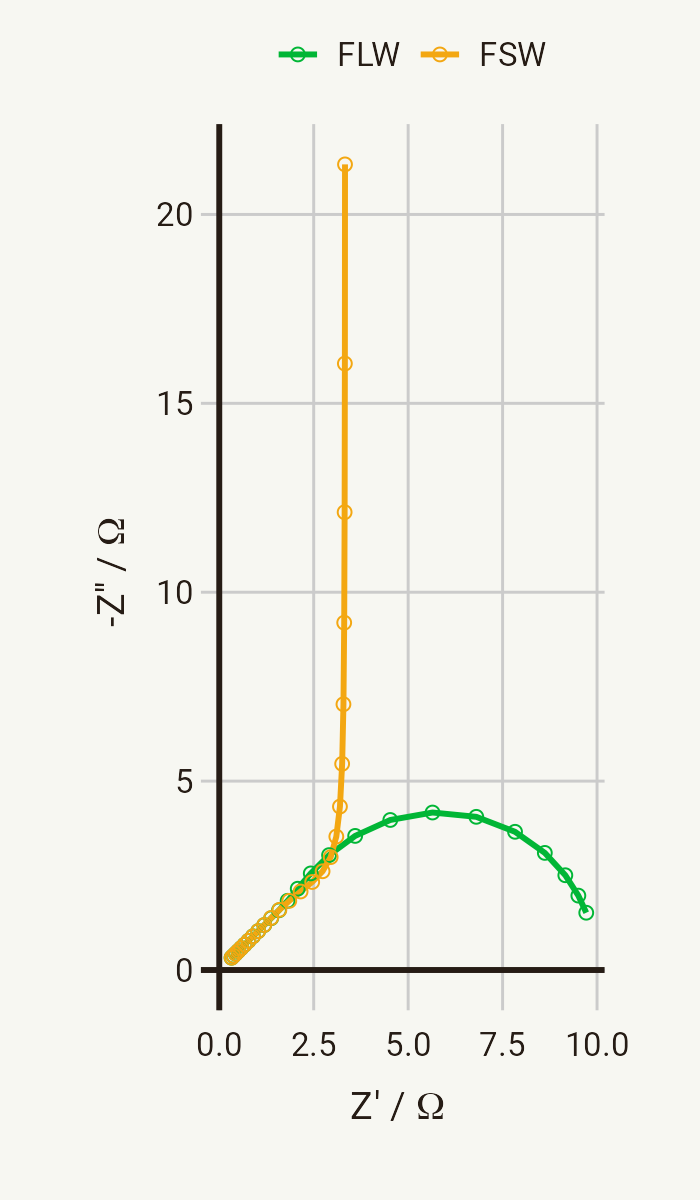
There are two important equivalent circuit elements for finite diffusion. They are the finite length Warburg (FLW) and the finite space Warburg (FSW), sometimes called the “short” and “open” Warburg elements respectively. Their responses in a Nyquist plot look like this, with parameters Z₀ = 10 Ω and $τ$ = 0.075 s (more on these parameters shortly) in the frequency range 10 kHz to 10 Hz:

Let’s look at the FLW first. Mathematically, it can be written as:

Z Z_{FLW} = Z_{0} {(j ω τ)}^{- 1 / 2} \tanh {(j ω τ)}^{1 / 2}

The two parameters $Z_{0}$ and $τ$ reflect the properties of the system or the process giving rise to the FLW behaviour. The impedance of the FLW tends to the value of $Z_{0}$ at low frequency. At high frequencies, the response is almost exactly that of the Warburg impedance. The shape of the FLW in the Nyquist plot therefore looks like a 45° line at higher frequencies, and transitions into a semi-circle shape at low frequencies. It can be thought of as a Warburg being “shorted” by a resistor - although a parallel W-R circuit will not give the same response. It can also be modelled by a finite length transmission line which is short-circuited at one end. For this reason it is sometimes also known as a “short Warburg”.

This response is typically associated with diffusion (or more generally mass transport) through a layer with a finite length. A classic example of this is the response of the rotating disk electrode - the point of which being to reduce the distance from the electrode to the bulk by controlling convection, rather than diffusion in this case.

The FSW has a rather similar definition:

Z Z_{FSW} = Z_{0} {(j ω τ)}^{- 1 / 2} \coth {(j ω τ)}^{1 / 2}

In this case, the response tends towards capacitive-like behaviour at low frequencies, where $Z^{'} (ω = \infty) = Z_{0} / 3$ . This response is typically associated with diffusion where one of the boundaries is blocking, such as in a porous electrode, as discussed previously on this page. This response is also associated with the diffusion of ions within a storage electrode, such as in lithium-ion batteries. This element can also be modelled as a finite length transmission line which is “open” at one end, and for this reason is sometimes also known as an “open Warburg”.

Mind the definitions!

You can find a number of different definitions of these finite elements and it’s easy to get confused. One source of confusion can be from defining these elements in terms of admittance. For example, the FLW is frequently defined like this:

Y Y_{FLW} = Y_{0} (j ω)^{- 1 / 2} \coth [B (j ω)^{- 1 / 2}]

You might have noticed that this definition contains $\coth$ instead of $\tanh$ . In this case it’s important to remember that:

\coth (x) = \frac{1}{\tanh (x)}